4.1 刚体的自由度
4.1.1 平面中刚体的自由度
刚体的自由度 (DOF) 已定义 作为它所拥有的独立运动的数量。图 4-1 显示平面中的刚体。确定此主体的自由度 我们必须考虑可以移动条形图的几种不同方式。在 一个二维平面,比如这个电脑屏幕,有3个自由度。 条形可以沿 x 轴平移,平移 沿 y 轴,并绕其质心旋转。
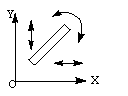
4.1.2 空间中刚体的自由度
空间中不受约束的刚体有六个自由度: 沿 x、y 和 z 轴的三个平移运动和分别围绕 x、y 和 z 轴的三个旋转运动。

4.2 运动约束
空间中的两个或多个刚体统称为刚体 身体系统。我们可以阻碍这些独立刚体的运动 具有运动约束的物体。运动 约束是刚体之间的约束,导致 刚体系统自由度的降低。
术语运动学对实际上是指刚体之间的运动学约束。运动学副 分为低对和高对,视两者如何 身体是接触的。
4.2.1 平面机构中的下对
平面机构中有两种下对:旋转对和棱柱对。
平面中的刚体只有三个独立的运动——两个 平移和一个旋转 — 所以引入一个旋转对 或两个刚体之间的棱柱对去除了两个度数 自由。
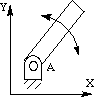

4.2.2 空间机制中的低对
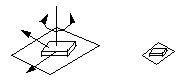
在空间机制类别下有六种低对。类型有:球面副、平面副、圆柱副、旋转 对、棱柱对和螺钉对。


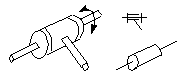

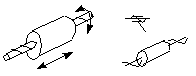
4.3 约束刚体
刚体和运动约束是 机制。受约束的刚体系统可以是运动链、机构、结构,也可以是这些都不是。 运动约束对刚体运动的影响 有两个内在的方面,即几何和物理 方面。换句话说,我们可以分析受约束的运动 刚体的几何关系或使用牛顿第二定律。
机构是一种受约束的刚体系统,其中 身体是框架。的度数 在考虑受约束的刚体系统时,自由度很重要 这是一种机制。当系统是 结构或当它没有确定的运动时。
计算刚体系统的自由度是直线的 向前。任何不受约束的刚体都有六个自由度 平面中的空间和三个自由度。添加运动学 刚体之间的约束将相应地减小 刚体系统的自由度。我们将讨论更多 下一节将介绍平面机制。
4.4 平面机构的自由度
4.4.1 格鲁布勒方程
机制自由度的定义 是刚体之间独立相对运动的次数。 例如,图 4-11 显示了 刚体受不同种类的对约束。

在图 4-11b 中,刚体受棱柱对约束,该棱柱对仅允许 平移运动。在二维中,它有一个度 自由,沿 x 轴平移。在此示例中, 身体失去了绕任何轴旋转的能力,并且无法移动 沿 y 轴。
在图 4-11c 中,刚体受到更高对的约束。它有两个度 自由度:沿曲面平移并绕 瞬时接触点。
一般来说,平面中的刚体有三个自由度。 运动学对是对刚体的约束,可降低 机制的自由度。图4-11所示为三种 平面机构中的对。这些对减少了度数 的自由。如果我们创建一个较低的对(图 4-11a,b),自由度将减少到 2。同样地 如果我们创建一个更高的对(图 4-11c),自由度降低到1。

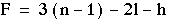
哪里
- F = 机构中的总自由度
- n = 链接数(包括 框架)
- l = 下对数(一个自由度)
- h = 高对数(两个自由度)
这个方程也被称为格鲁布勒方程。
示例 1
请看图4-13a中门上方的横梁。开幕式和 关闭机构如图4-13b所示。让我们计算一下它的 自由度。
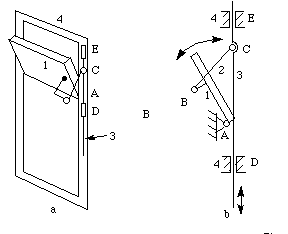
图4-13 横梁机构
n = 4(链接 1、3、3 和帧 4),l = 4(在 A、B、C、D 处),h = 0

注意:D 和 E 作为同一棱柱对起作用,因此它们仅 算作一对较低的对。
示例 2
计算图4-14b所示机构的自由度。 图4-14a是该机制的应用。

图4-14 自卸车
n = 4, l = 4 (在 A, B, C, D), h = 0

示例 3
计算图4-15所示机构的自由度。
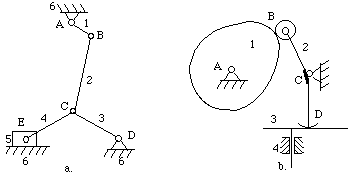
图4-15 自由度计算
对于图4-15a中的机制
n = 6, l = 7, h = 0

对于图4-15b中的机制
n = 4, l = 3, h = 2

注意:滚筒的旋转不影响 机构的输入和输出运动的关系。因此 不考虑滚筒的自由度;它被称为被动或冗余自由度。 想象一下,在计算度数时,滚子被焊接到连杆 2 上 机制的自由度。
4.4.2 库茨巴赫准则
机构的自由度数 也称为设备的移动性。迁移率是输入参数的数量(通常为对 变量),必须独立控制才能带来设备 到特定位置。库茨巴赫准则, 类似于 Gruebler 方程, 计算流动性。
为了控制一个机构,独立输入的数量 运动必须等于机械装置的自由度数。 例如,图 4-13a 中的横梁具有单一的自由度,因此它需要一个独立的输入 打开或关闭窗口的动作。也就是说,您只需推或拉杆 3 操作窗口。
再看一个例子,图中的机制 4-15A 也有 1 个自由度。如果独立输入是 应用于连杆 1(例如,电机安装在接头 A 上以驱动 链接 1),该机构将具有规定的运动。
4.5 有限变换
有限变换用于描述点的运动 刚体和刚体本身的运动。
4.5.1 有限平面旋转变换

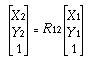
哪里
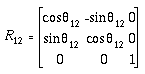
4.5.2 有限平面平移 转型

 x,
x,  y)。我们可以这样描述 使用平移运算符 T12 的运动:
y)。我们可以这样描述 使用平移运算符 T12 的运动:
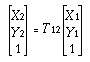
哪里
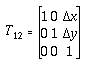
4.5.3 有限平面位移的串联
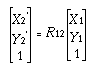
和
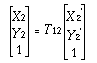
我们可以将这些动作连接起来,得到

其中 D12 是平面一般位移算子:

4.5.4 平面刚体变换
我们已经讨论了各种转换来描述 刚体上点的位移。这些运算符可以 应用于点系统的位移,例如刚性 身体?
我们使用 3 x 1 齐次列矩阵来描述向量 表示单个点。平面 3 x 3 的有益特性 平移、旋转和一般位移矩阵算子 是它们可以很容易地在计算机上编程以操纵 3 x n 个列向量的矩阵,表示刚体的 n 个点。 由于刚体的每个粒子彼此之间的距离 刚体的点是常数,向量定位每个点 的刚体必须经历相同的变换,当刚体 主体移动并指定正确的轴、角度和/或平移 来表示其运动。(桑多尔 &Erdman 84)。例如,一般平面变换 对于刚体上的三个点 A、B、C 可以表示 由
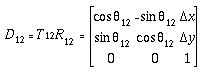
4.5.5 空间旋转变换
我们可以描述一个用于旋转的空间旋转算子 围绕单位轴 u 的点的变换 坐标系的原点。假设点的旋转角度 关于你是  , 旋转运算符将由下式表示
, 旋转运算符将由下式表示
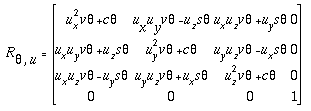
哪里
- ux、uy、uz 是耳形 单位轴 U 分别在 X、Y 和 Z 轴上的投影。
- s
 = 罪
= 罪
- c
 = 因为
= 因为
- v
 = 1 – 余弦
= 1 – 余弦
4.5.6 空间平移变换
假设刚体上的点 P 穿过 翻译描述从 P1 到 P2 的直线路径,坐标变化为 ( x, y,
x, y, 
 z),我们可以描述这一点 使用平移运算符 T 的运动:
z),我们可以描述这一点 使用平移运算符 T 的运动:
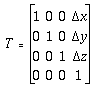
4.5.7 轴的空间平移和旋转矩阵 通过原点,
假设刚体上的点 P 以角度旋转 关于单位轴 u 的位移 穿过 的原点 首先是坐标系,然后是沿 u 的平移 Du。这种旋转的组成 转换,这种转换是螺丝钉 运动。其对应的矩阵算子,螺杆 运算符,是等式 4-7 中的平移运算符和等式 4-9 中的旋转运算符的串联。

4.6 刚体之间的变换矩阵
4.6.1 两个 Arbitray 之间的变换矩阵 刚体
对于刚体系统,我们可以建立局部笛卡尔 每个刚体的坐标系。变换矩阵是 用于描述刚体之间的相对运动。
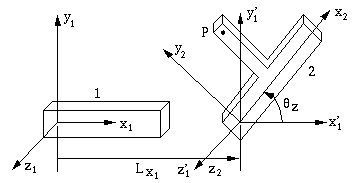
例如,空间中的两个刚体各具有局部坐标 系统 x 1 y 1z1和 x 2 y 2z2.设点 P 为 附着在位置的主体 2 (x 2, y2, z 2) 在主体2 的局部坐标系中。要查找 P相对于物体1局部坐标系的位置, 我们知道,点 x 2 y 2z2 可以从x 1 y 1 z1获得,如下式 沿 x 轴组合平移 Lx1 和 旋转 Z 关于  Z 轴。我们可以推导如下变换矩阵:
Z 轴。我们可以推导如下变换矩阵:

如果刚体 1 固定为框架,则 可以在此主体上创建全局坐标系。因此, 上面的变换可用于映射 指向全局坐标。
4.6.2 两个刚性之间的运动约束 机构
上面的变换矩阵是两个的具体示例 不受约束的刚体。转换矩阵取决于 两个刚体的相对位置。如果我们连接两个刚性 具有运动约束的物体,其 自由度将降低。换句话说,他们的亲戚 运动将在某种程度上被指定。
假设我们用一对旋转对约束上面的两个刚体,如图 4-19 所示。我们可以 仍然以与等式 4-18 相同的形式编写变换矩阵。
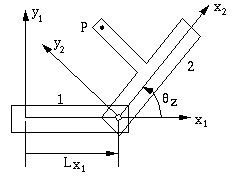
图4-19 约束体上点的相对位置
区别在于 Lx1 是一个常数 现在,因为 Revolute 对固定了坐标系的原点 x 2 y 2z2相对于坐标系 x 1 y 1z1.但是,旋转  z 仍然是一个变量。因此,运动学约束指定 在某种程度上是变换矩阵。
z 仍然是一个变量。因此,运动学约束指定 在某种程度上是变换矩阵。
4.6.3 Denavit-Hartenberg表示法
Denavit-Hartenberg 符号 (Denavit & Hartenberg 55) 是 广泛用于联动坐标系和机器人机构的变换。它可以是 用于表示链接之间的转换矩阵,如 图 4-20。

在此图中,
- zi-1 和 zi 是两个旋转对的轴;
 i 是轴 xi-1 和 xi 的夹角;
i 是轴 xi-1 和 xi 的夹角;- di 是坐标系原点之间的距离 x i-1 y i-1 zi-1和脚的共同点 垂直;
- ai 是公共垂直线两英尺之间的距离;
 i 是轴 zi-1 和 zi 的夹角;
i 是轴 zi-1 和 zi 的夹角;
变换矩阵为 T(i-1)i
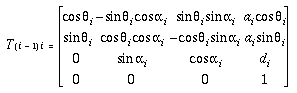
上述变换矩阵可以表示为 T(a i, i,  i,
i,  d i) 为方便起见。
d i) 为方便起见。
4.6.4 变换矩阵在链接中的应用
连杆由几个受约束的刚体组成。就像一个 机制,一个连杆应该有一个框架。矩阵方法可以是 用于推导连杆的运动学方程。如果所有 链接形成一个闭环,所有 变换矩阵将是一个单位矩阵。如果机制 有 N 个链接,我们将有:
T12T23…T(n-1)n = I

