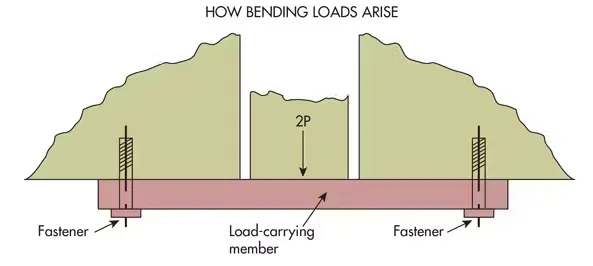
安装在承重构件末端或边缘附近的紧固件通常承载的不仅仅是施加的载荷。它们还承载着由承重构件的弯矩产生的隐藏载荷。这种额外的负载可能会大大超过施加的负载。
当将中心负载 (2P) 施加在靠近两端的承载构件上时,构件的末端往往会向上弯曲。相邻构件施加的约束会产生轴承载荷,从而增加紧固件承载的载荷。这种轴承载荷可能明显大于施加的载荷。
如果下图中的承载构件具有无限刚性,则紧固件将只需要抵抗施加的 2P。但在大多数应用中,会产生不同的负载条件。承载构件的柔韧性通常要求边缘或端部能够抵抗由局部载荷引起的角旋转。
在此分析中,假设轴承载荷在边缘处达到最大值,在紧固件中心线处逐渐变细至零,荷载分布呈三角形。在这些条件下,紧固件载荷和应力为:
σmax = 24sm/(8ws3 – 4R3)
P1 = 最大 σ/6 秒(3ws2 – 4R3)
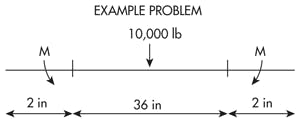
一个 5 英寸宽的杆中央加载 10,000 磅的力。紧固件中心线之间的距离为 36 英寸,杆在两端延伸出紧固件中心线 2 英寸。
为了使用这些方程,M(由轴承载荷产生的电阻矩)被保守地设置为等于维持承载构件的固定端约束所需的弯矩。然后,第一个方程确定最大轴承应力,第二个方程确定紧固件上的合力轴承载荷。
示例:一根 5 英寸宽的棒材由 10,000 磅的力集中加载,两端由穿过半径为 0.5 英寸的孔的紧固件约束。孔中心线之间的距离为 36 英寸,紧固件中心线与杆端之间的距离为 2 英寸。紧固件上的最大轴承应力和最大载荷是多少?
从材料的基本强度,
M = 2PL/8 = 10,000(36)/8 = 45,000 英寸磅
然后从第一个方程中找到最大应力为:
σ最大 = 24(2)(45,000)/[8(5)(2)3 – 3π(0.5)4
= 6,800 psi
根据第二个方程,轴承载荷为:
P1 = 6,800/6(2) [3(5)(2)2 – 4(0.5)3]
= 33,700 磅
因此,紧固件上的最大载荷是轴承载荷加上施加载荷的一半,即 38,700 磅。
命名法:
- L 是紧固件中心线之间的距离,in。
- M 是轴承载荷提供的电阻矩,单位为 lb。
- P 是承重构件上总载荷的一半,lb.P
- 1 是紧固件上的合力轴承载荷,lb.R
- 是紧固件孔的半径,in。
- s 是从紧固件中心线到承载构件末端的距离,in。
- w 是承载构件的宽度,in。
- σmax 是最大轴承应力 psi。