- 凸轮(cam):通常作主动件作等速转动
- 推杆(从动件,follower):被凸轮直接推动的构件
- 反凸轮机构(inverse cam mechanism):凸轮为从动件
凸轮机构的分类:
按凸轮形状
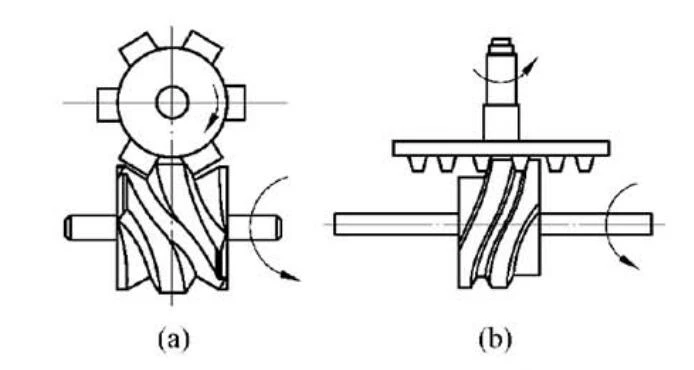
- 盘形凸轮:一个具有变化向径的盘形构件绕固定轴线回转
- 圆柱凸轮:在圆柱面上开有曲线凹槽,或在圆柱端面上作出曲线轮廓

按推杆形状
- 尖顶推杆:构造最简单,但易磨损
- 滚子推杆:摩擦较小,可用来传递较大的动力
- 平底推杆:凸轮与平底的接触面间易形成油膜,润滑性好,常用于高速传动
按推杆运动形式
- 直动推杆
- 对心直动推杆
- 偏置直动推杆
- 摆动推杆
按凸轮与推杆保持接触的方法不同
- 力封闭:利用推杆的重力、弹簧力来使推杆与凸轮保持接触
- 几何封闭:利用凸轮或推杆的特殊几何结构使保持接触
- 沟槽凸轮、
- 等宽凸轮机构
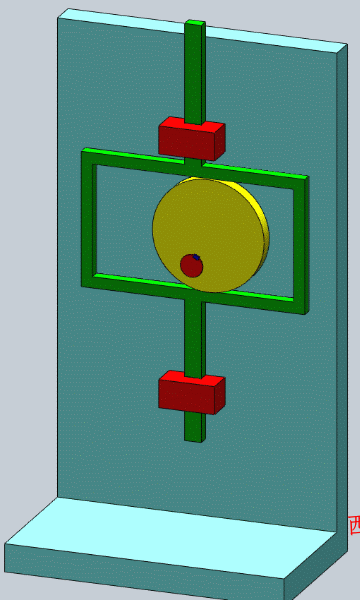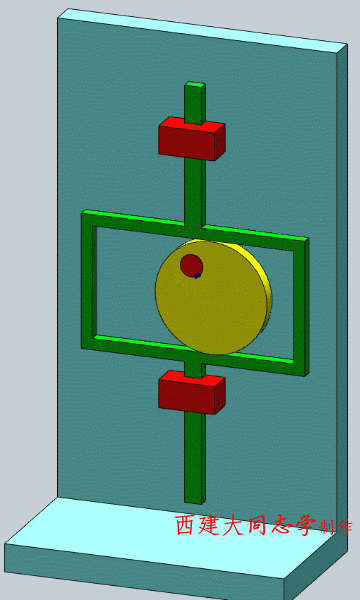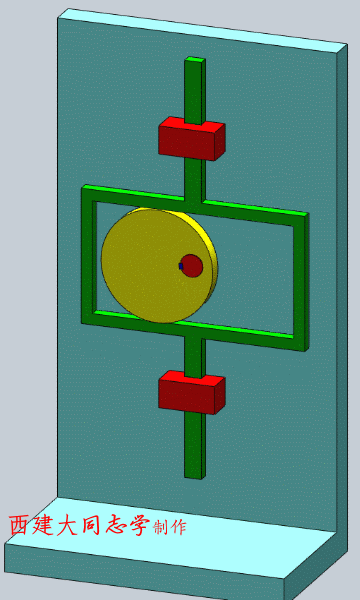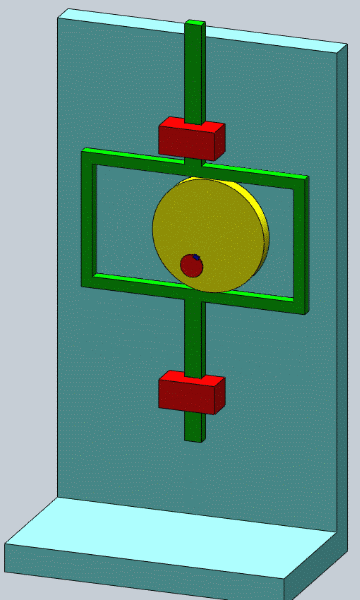
- 等径凸轮机构
- 共轭凸轮(主回凸轮,conjugate cam)
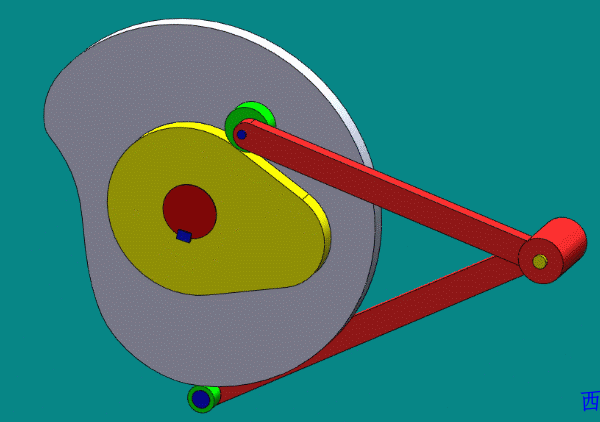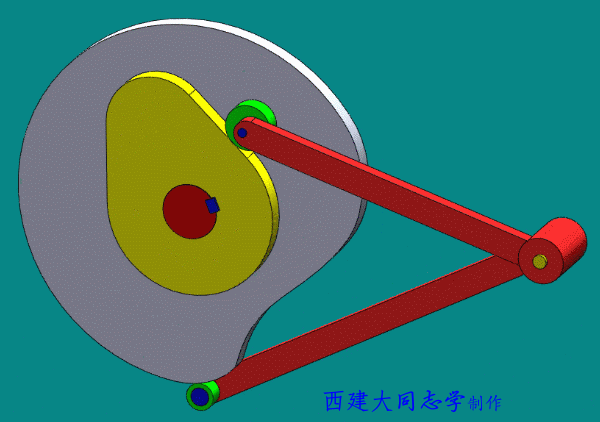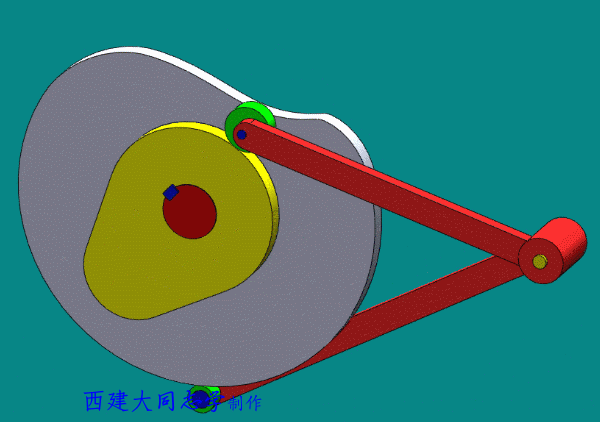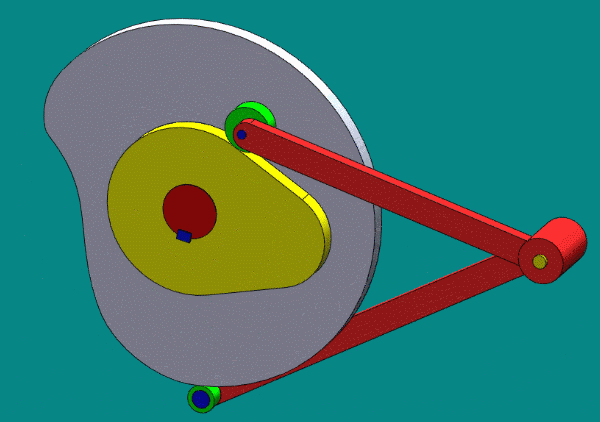
推杆的运动规律
| 符号 | 说明 | |
|---|---|---|
| 基圆 | 𝑟0r0 | 以凸轮最小半径所做的圆 |
| 推程运动角 | 𝛿0δ0 | 推杆由最低位置被推到最高位置(推程)对应的凸轮转角 |
| 远休止角 | 𝛿01δ01 | 推杆在最高位置静止不动(远休止)对应的凸轮转角 |
| 回程运动角 | 𝛿0′δ0′ | 推杆由最高位置回最低位置(回程)对应的凸轮转角 |
| 近休止角 | 𝛿02δ02 | 推杆在最低位置静止不动(近休止)对应的凸轮转角 |
| 推程 | ℎh | 推杆在推程或回程中移动的距离 |
推杆运动规律:
推杆的位移 𝑠s 、速度 𝑣v和加速度 𝑎a 随凸轮转角 𝛿δ 变化的规律
刚性冲击:
速度突变,推杆理论上将出现无穷大的加速度和惯性力
柔性冲击:
加速度有突变,但为有限值,引起的冲击较小
多项式运动规律:
- 一般表达式:
𝑠=𝐶0+𝐶1𝛿1+𝐶2𝛿2+…+𝐶𝑛𝛿𝑛s=C0+C1δ1+C2δ2+…+Cnδn
- 𝛿δ —— 凸轮转角
- 𝑠s —— 推杆位移
- 𝐶0C0 、𝐶1C1、 𝐶2C2、… 、 𝐶𝑛Cn —— 待定系数,利用边界条件等来确定
- 一次多项式运动规律:
- 等速运动规律
- 有刚性冲击
- 二次多项式运动规律:
- 等加速等减速运动规律
- 有柔性冲击
- 五次多项式运动规律:
- 无刚性冲击、无柔性冲击
三角函数运动规律
- 余弦加速度运动规律/简谐运动规律
- 有柔性冲击、无刚性冲击
- 正弦加速度运动规律/摆线运动规律
- 无刚性冲击、无柔性冲击
- 加速度最大值最大
凸轮轮廓曲线的设计
设计方法所依据的基本原理:反转法
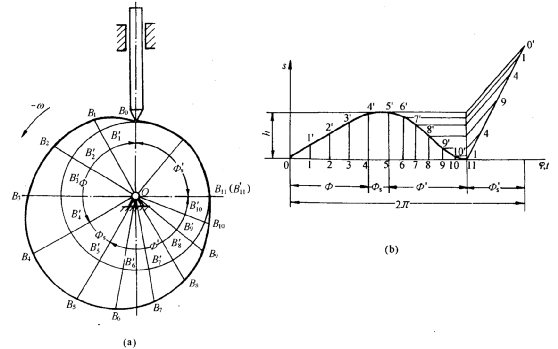
设计方法:图解法、解析法
理论廓线(cam pitch curve):
- 滚子中心A在推杆复合运动中的轨迹
- 凸轮的基圆半径若未指明,通常系指理论廓线的最小半径
实际廓线(cam contour):
- 又称工作廓线
- 以理论廓线上一系列点为圆形,以滚子半径 𝑟𝑟rr 为半径,作一系列的圆,再作此圆族的包络线,即为凸轮的实际廓线
- 理论廓线向外延伸一个滚子半径长度得到的廓线
凸轮机构基本尺寸的确定
基圆半径、滚子半径、平底尺寸、压力角
压力角
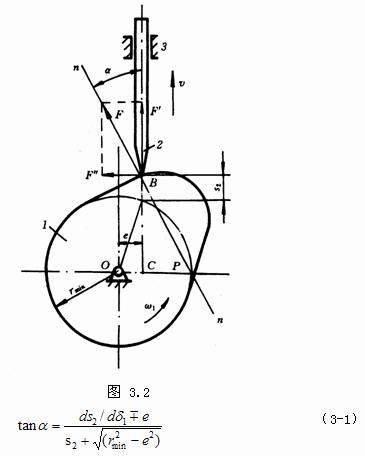
- 推杆沿凸轮廓线接触点的法线方向与推杆速度方向之间所夹的锐角
- 临界压力角𝛼𝑐αc𝛼𝑐=arctan[1/(1+2𝑏𝑙tan𝜑2)]−𝜑1αc=arctan[1/(1+l2btanφ2)]−φ1通过增大导轨长度l,减小悬臂尺寸b,可以提高临界压力角
- 许用压力角[a]
- 推程时:
- 直动推杆[𝛼][α] = 30°
- 摆动推杆[𝛼][α] = 30° ~ 45°
- 回程时:70° ~ 80°
- 推程时:
基圆半径的确定:
在偏距一定、推杆的运动规律已知的条件下,加大基圆半径 𝑟0r0 可以减小压力角 𝛼α ,从而改善机构的传力特性,但此时机构的尺寸将会增大。
变尖与失真:
- 理论廓线曲率半径 𝜌ρ ;滚子半径 𝑟𝑟rr;工作廓线曲率半径 𝜌𝑎ρa;𝜌𝑎=𝜌+𝑟𝑟ρa=ρ+rr
- 如果 𝜌=𝑟𝑟ρ=rr ,𝜌𝑎ρa = 0,工作廓线出现尖点,称为变尖现象
- 当 𝜌<𝑟𝑟ρ<rr , 工作廓线出现交叉,致使推杆不能按预期的运动规律运动,称为失真现象