1 物理原理
本章介绍其背后的基本物理原理 ,为此所需的机制以及基本概念和原则 。
1.1 力和扭矩
1.1.1力
力:一种代理或影响,如果应用于自由 身体主要导致身体加速,有时在 弹性变形等影响。
我们每天都在与这样或那样的力量打交道。一个 压力是一种力。地球对所有人施加着吸引力 其表面上的物体或物体。研究作用在 物体,我们必须知道力是如何施加的,方向 力量及其价值。从图形上看,力通常用 向量,其末端表示作用点。
机制是负责任何动作或反应的东西。机器基于通过传递力的想法 一系列预定的运动。这些相关概念是 动态运动的基础。
1.1.2扭矩
力矩:产生或倾向于产生旋转的东西 其有效性由力的乘积和 从力的作用线到 旋转轴。
考虑图 1-1 中所示的杠杆。杠杆 是绕不动点A自由转动的柱线,称为支点;重物作用在杠杆的一侧,平衡 力作用在杠杆的另一侧。
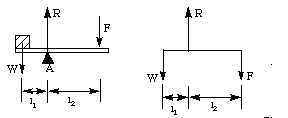
图1-1 具有平衡力的杠杆
要分析杠杆,我们需要找到 作用在杠杆上的力。获得力 W 的扭矩约为 点 A,将 W 乘以 l1,即其距离 一个。类似地,F x l2 是 F 的转矩 大约 支点A.
1.2 运动
运动:位置或方向的改变。
1.2.1 沿直线路径运动
我们从最简单的情况开始研究运动,即 直线。
- 沿一条线
的位置和位移 研究运动的第一步是描述一个 移动对象。考虑一辆汽车在东西向的直道上行驶 公路。我们可以用以下方式描述汽车的位移 说“车在中心镇以西5公里处”。在这个 描述中,我们指定了两个因素,即原始测量点 和位移的方向。 - 速度
我们可以定义物体稳定移动的速度 单位时间位移:
(1-1)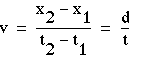
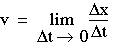
(1-2) - 加速度 加
速度是单位时间内速度的变化 时期。如果速度以恒定速率变化,那么我们可以 用(1-3)
描述加速度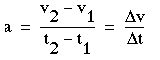
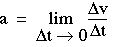
(1-4)
1.2.2 空间中的直线运动
当运动不仅仅是 沿着一条直线,而是延伸到一个平面上。在这里,我们 可以用一个矢量来描述运动,该矢量包括大小和 运动的方向。
- 位置矢量和位移矢量
描述对象位置的有向线段 相对于原点是位置向量,如 d 1 和 d2 在<a=href”#hdr8″>数字 1-2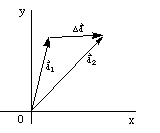
图 1-2位置矢量和位移矢量
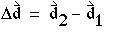
(1-5) - 速度矢量
对于 发生在 时间间隔
发生在 时间间隔  t, 间隔期间的平均速度为
t, 间隔期间的平均速度为
(1-6)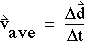
 d。在 delta t 接近零的极限中,瞬时速度为
d。在 delta t 接近零的极限中,瞬时速度为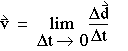
(1-7)V的方向是d的方向 ,对于非常小的方向 位移;因此,它沿着路径或与路径相切。
,对于非常小的方向 位移;因此,它沿着路径或与路径相切。
- 加速度矢量
瞬时加速度是 v / t比
t比 值的极限,因为
值的极限,因为 t变得非常小:(1-8)
t变得非常小:(1-8)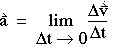
1.2.3 刚体在平面上的运动
前面的章节讨论了粒子的运动。对于刚性 物体在平面上,它的运动通常比粒子更复杂 因为它由直线运动和旋转运动组成 运动。一般来说,这种运动可以分解成两种 运动(图 1-3),它们是:
- 刚体质心的直线运动。在 这部分运动,该运动与运动相同 平面上的粒子。
- 刚体的旋转运动相对 到它的质心。
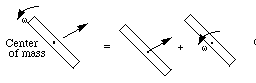
图 1-3 刚体在平面中的运动
1.3 牛顿运动定律
1.3.1 牛顿第一定律
当没有力施加在物体上时,它会保持静止或以 匀速直线。这种惯性原理也是 被称为牛顿第一定律。正是从这条法律中, 牛顿能够建立起我们目前对动力学的理解。
1.3.2 牛顿第二定律
从我们的日常生活中,我们可以观察到:
- 当 力 F 施加在物体上,V,
 变化 物体的速度,随着时间的长度而增加 t. 增加;
变化 物体的速度,随着时间的长度而增加 t. 增加; - 力 F 越大,V 越大
 ;和
;和 - 物体(物体)越大,越不容易被力加速。
将 F t 和
t 和  V 之间的比例写成以下形式很方便:
V 之间的比例写成以下形式很方便:
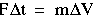
比例常数 m 随对象而变化。这 常数 m 称为惯性质量 身体。上述关系体现了牛顿定律 运动(牛顿第二定律)。如
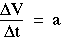
其中 a 是物体的加速度。我们有
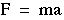
如果 m = 1 kg 和 a = 1m/sec2,则 F = 1 牛顿。
力和加速度是矢量,牛顿定律可以写成 以矢量形式。
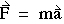
1.4 动量和动量守恒
1.4.1 脉冲
尝试让棒球和炮弹以相同的速度滚动。 正如你所猜到的,让炮弹前进更难。如果你 在时间  t 上施加恒定力 F,即速度的变化 由公式 1-9 给出。因此,要获得相同的
t 上施加恒定力 F,即速度的变化 由公式 1-9 给出。因此,要获得相同的  v, 产品 F
v, 产品 F t 您尝试加速的质量 m 必须越大。
t 您尝试加速的质量 m 必须越大。
从静止处投掷炮弹并赋予它相同的最终速度 作为棒球(也是从休息开始),我们必须更加努力或 长。重要的是产品F t。本产品 F
t。本产品 F t 是 自然地衡量我们推动改变 运动。它被称为力的冲动。
t 是 自然地衡量我们推动改变 运动。它被称为力的冲动。
1.4.2 动量
假设我们对棒球和大炮施加相同的冲动 球,两者最初都处于静止状态。由于量 mv 的初始值在每种情况下都为零,并且由于相等的脉冲 应用后,棒球的最终值 mv 将相等,并且 炮弹。然而,因为炮弹的质量很大 大于棒球的质量,大于炮弹的速度 将远小于棒球的速度。因此,乘积 mv 是运动的完全不同的度量 而不仅仅是 V。我们称它为物体的动量p,并以千克米每秒为单位进行测量。
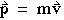
速度和动量相当 不同的概念:速度是一个运动学量,而 动量是动态的,与变化的原因有关 在群众的运动中。
由于它与牛顿定律中自然发生的冲量(方程 1-9)有关,我们期望动量自然地适合牛顿动力学。牛顿做到了 用动量来表达他的运动定律,他 称为运动量。我们可以用 动量变化而不是速度变化的术语:
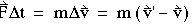
其中 v 和 v‘ 是 冲动。最后一个方程的右边可以写成
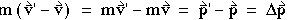
动量的变化。因此
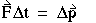
或者,换句话说,冲动等于动量。
1.4.3 动量守恒
在图 1-4 中,一个移动的台球发生碰撞 台球休息。入射球停止,球停止 击球的速度与入射球的速度相同 在。两个台球的质量相同。因此,第二个球之后的动量 碰撞与之前入射球的碰撞相同 碰撞。事件球已经失去了所有的动力,而 它击中的球恰好获得了 事故球丢失了。
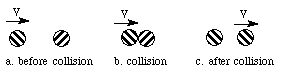
图 1-4台球碰撞
这种现象符合守恒定律 动量,表示总动量是恒定的 当两个身体相互作用时。
1.5 功、功率和能源
1.5.1 工作
功是施加在一定距离上的力。如果拖动 沿着地板的物体,你努力克服摩擦 在物体和地板之间。在举起物体时,您确实会抵抗重力,重力往往会将物体拉向 地球。机车气缸中的蒸汽在膨胀时确实起作用 并推动活塞抵抗阻力。功是克服阻力和通过距离的产物 它被克服了。
1.5.2 电源
功率是完成工作的速率。
在英国系统中,功率以英尺磅每秒表示。 对于较大的测量,使用马力。
1 马力 = 550 英尺 *磅/秒 = 33,000 英尺*磅/分钟
以 SI 单位表示,功率以焦耳/秒为单位,也称为 瓦特 (W)。
1hp = 746 W = 0.746kW
1.5.3 能源
所有物体都拥有能量。这可能来自完成的工作 在某个时间点。一般来说,有两种 机械系统中的能量,势能和动能。 势能是由于物体的位置和 动能是由于它的运动。
例如,一个运动中的物体可以克服一定数量的 抵抗在被休息之前,以及 由于其运动,物体在克服 阻力,使物体静止。 发动机上的飞轮 两者都接收和放弃能量,从而使能量在整个中风过程中更顺利地返回。
升高的重量有做功的力量 说明它们的高位,如各种类型的锤子等。

