1. 引言
凸轮机构是生产机器和设备设计的基本对象之一,其特点是生产和工作过程的高度自动化和优化。这些机械系统的特点是在高速下传递大负载的可能性和相关机械工作部件的位置精度。它们的应用主要与所谓的硬自动化有关,其特征是给定技术设备的操作不可更改或难以更改。它们在制造业的制造和搬运机械中的广泛使用是众所周知的,它们的动态效果和性能极大地影响了此类机械的整体行为、操作和效率。目前,对此类机械的性能参数的要求越来越高。因此,运动体的运行速度和惯性效应增加,从而降低了机器的可用运行频率。这些事实会导致更大的磨损,并降低机器的整体寿命和可靠性,在设计和开发它们时必须考虑到这一点。计算机技术、数值数学和信息学的发展使得分析和数值方法在凸轮机构的设计、开发和构建中使用成为可能。
一般凸轮机构通常称为具有单自由度的三连杆机构,它由安装在固定框架(1)上的两个移动构件组成。移动部件是凸轮(2)和从动件(3)(参见图1).在一般凸轮机构的情况下,一般运动学对由凸轮的工作面和从动件的接触形成。所述类型的运动学对的接触区域表面的接触应变,以及在该表面附近,具有周期性过程。由于接触应变作用,接触面上会发生疲劳损伤。这种损伤的标准之一可能是接触区域及其附近最大压缩主应力的值。随后,这与相应材料的强度极限有关。凸轮机构的使用寿命与材料的选择及其制造各个部件的物理和机械性能、材料加工方法以及单个零件的制造技术或负载的方式和强度密切相关。它也与加载的方式、强度和条件有关。这个问题将理论力学、应用力学和接触力学、摩擦学、材料工程和结构分析的知识联系起来,尽管这些理论知识必须得到实验鉴定结果的支持。
在技术实践中,除了基本的三体凸轮系统外,还经常遇到多体凸轮系统,三体凸轮系统还可能包含变速连杆和恒定传动比的机构。这种机械系统称为凸轮铰链或组合凸轮机构。这些具有单一自由度的机械系统的特点是驱动部件的运动均匀,在大多数应用中通常不需要凸轮。凸轮工作面的形状实现了系统工作部件的工作运动,不一定是从动件。在许多情况下,静动力分析方法足以基本确定这些机械系统动态行为的时间过程。动静力解决方案确定驱动力效应、关节中的反作用力以及凸轮机构和连杆传递的力效应。对于解决方案,必须了解机构所有成员的运动量和几何质量参数以及作用在单个物体上的作用力效应。因此,静动分析的结果成为确定凸轮和从动件接触区域内接触应力分布的基本数据。
2. 凸轮机构
本节仅提供有关如何解决组合凸轮机构任务的基本信息。指定了研究此类机械系统的基本术语和分析方法。例如,运动学分析和综合的结果进一步用于这些机械系统的运动静压或动态分析任务。这些分析的主要目的是确定运动学对中的反应过程、凸轮和从动件的力载荷、作用在单个构件上的力效应、系统运动所需的驱动效应等。了解凸轮机构一般运动副中的作用力对于确定凸轮和从动件接触中的接触应力分布非常重要。
2.1 通用凸轮机构
根据定义,通用凸轮机构是指具有单自由度的三连杆机械系统,其中包含至少一个凸轮,通过至少一个通用运动对与其他构件连接。在这种情况下,一般运动对是通过接触凸轮和从动件形成的,其运动是平移、旋转或一般。凸轮机构可以在非常精确的规定路径内实现所需的工作运动,只需使用容纳在相对较小的空间内的少量主体。凸轮是驱动(或输入)部件;在形状方面,可以定义基本的凸轮类型:径向、轴向(圆柱形)和球形。从动件被称为凸轮机构的驱动(或输出或工作)部件,它执行所需的运动。平移跟随运动被定义为平移或一般运动。执行旋转运动的旋转从动件通常称为杠杆。为了降低被动阻力,在技术实践中,从动件通常配备滚轮,从而在凸轮轮廓和从动件之间的相互作用中发生纯滚动,如图所示图1.这种安排不会影响所需的跟随运动。
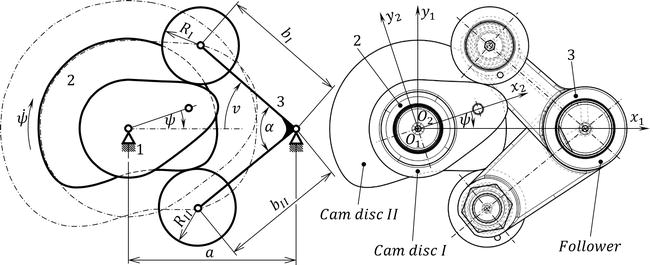
凸轮机构正常运行的主要条件之一是在动作过程中保持从动件与凸轮的永久接触。一般运动学对的这种约束是通过载荷或冗余运动学约束实现的。在第一种情况下,使用预紧的可回收压缩弹簧、重力或内置液压或气动元件来保持给定的接触。这种布置的缺点是凸轮机构的力载荷和磨损增加,这是由从动件和凸轮之间永久接触所需的预紧力引起的。在第二种情况下,通过添加额外的连杆来确保冗余约束的接触。例如,带槽的凸轮可以实现这样的布置。本实施例简单,但其缺点是滚子在滚子从动件与凸轮之间的相对运动过程中,滚子在凸轮槽中的旋转方向发生变化。这种现象是由滚子和凸轮槽之间传递的法向反作用力感的变化引起的,因为在凸轮机构操作过程中相对运动的极点发生了变化。结果,凹槽的工作面在滚子旋转变化点上磨损更大。双凸轮和滚柱从动系统是凸轮机构的更优选设计,具有冗余运动学约束,尽管这种解决方案更昂贵且制造起来更复杂。共轭、互补或双盘凸轮是包括双径向盘的凸轮,每个径向盘与至少两个通过刚性或运动连杆耦合的从动从动件接触。这种机构的移动性由特殊的尺寸布置确保,其中双凸轮的两个工作表面的作用必须彼此完全对应。带有径向共轭凸轮和摆动双滚柱从动件的凸轮机构示意图如图所示图1.给定的约束由另一个径向凸轮 II 和一个滚柱从动件 II 组成。
凸轮轮廓的形状是通过综合确定的,该综合是在给定凸轮机构的位移定律及其尺寸参数的基础上确定的。凸轮相对于凸轮机构框架的位置由角度变量确定 ψ𝜓 ,跟随者的位置用广义变量表示 v𝑣 (见图1).
2.2 组合凸轮机构
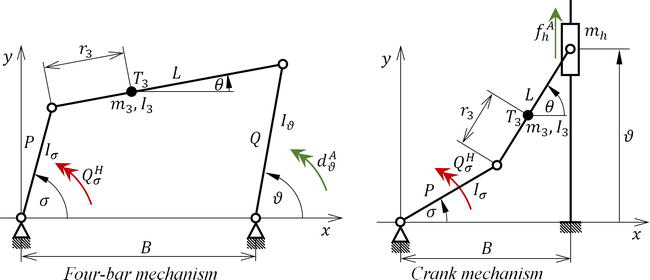
作为组合凸轮机构,它通常被称为机械系统,通常具有单一自由度,其中至少包括一个通用凸轮机构。该系统通常还包括各种变速连杆组,这些连杆不仅具有恒定的齿轮比,而且具有通常可变的齿轮比。它们通常由与较低运动学对的简单连接来补充。在实践中,下对通常是两个可移动的调整相邻构件之间的平面耦合。通过运动学对与框架连接的杆件称为变换连杆的基本杆件。它们执行旋转或平移运动。这种机构的基本代表是四杆机构、曲柄机构、摆动机构、齿轮等(参见图2).根据已发表的知识,提出了以下研究结果 [1,3,4]:
相关链接的输入是变量的有序三元组 σk=(σk,σ̇ k,σ¨k)𝜎𝑘=𝜎𝑘𝜎̇𝑘𝜎¨𝑘 表示机械系统输入链路的运动。输出是变量的三元组 ϑk=(ϑk,ϑ̇ k,ϑ¨k)𝜗𝑘=𝜗𝑘𝜗̇𝑘𝜗¨𝑘 ,表示同一系统的输出链路的运动。指数 k𝑘 表示相关联系的数字指示,在案文的下一部分将忽略它。链接的一般方程可以定义为隐函数,其中位置大小 σ𝜎 , ϑ𝜗 的基本成员与时间有关:
F(σ,θ)=0,σ=σ(t),θ=θ(t)𝐹𝜎𝜗=0,𝜎=𝜎𝑡,𝜗=𝜗𝑡 E1型
通过差异化式 (1)随着时间的流逝,速度和加速度之间的关系可以得到:
∂F∂σσ ̇+∂F∂ϑϑ ̇=0,∂F∂σσ¨+∂2F∂σ2σ ̇2+2∂2F∂σ∂ϑσ ̇ϑ ̇+∂F∂ϑϑ¨+∂2F∂ϑ2ϑ ̇2=0𝜕𝐹𝜕𝜎𝜎̇+𝜕𝐹𝜕𝜗𝜗̇=0,𝜕𝐹𝜕𝜎𝜎¨+𝜕2𝐹𝜕𝜎2𝜎̇2+2𝜕2𝐹𝜕𝜎𝜕𝜗𝜎̇𝜗̇+𝜕𝐹𝜕𝜗𝜗¨+𝜕2𝐹𝜕𝜗2𝜗̇2=0 E2型
相对于时间的微分用点 in 表示式 (2).连杆比称为大小,取决于连杆的位置,由下式给出式 (3):
dθdσ=−∂F∂σ(∂F∂ϑ)−1,dσdθ=−∂F∂ϑ(∂F∂σ)−1dθdσ=−𝜕𝐹𝜕𝜎𝜕𝐹𝜕𝜗−1,dσdθ=−𝜕𝐹𝜕𝜗𝜕𝐹𝜕𝜎−1 E3系列
的衍生物式 (3)关于职位由下式给出式 (4):
d2ϑdσ2=−[∂2F∂σ2+2∂2F∂σ∂ϑ⋅dθdσ+∂2F∂ϑ2(∂ϑ∂σ)2](∂F∂ϑ)−1,𝑑2𝜗dσ2=−𝜕2𝐹𝜕𝜎2+2𝜕2𝐹𝜕𝜎𝜕𝜗·dθdσ+𝜕2𝐹𝜕𝜗2𝜕𝜗𝜕𝜎2𝜕𝐹𝜕𝜗−1,
d2σdθ2=−[∂2F∂ϑ2+2∂2F∂σ∂ϑ⋅dσdθ+∂2F∂σ2(∂σ∂ϑ)2](∂F∂σ)−1𝑑2𝜎dθ2=−𝜕2𝐹𝜕𝜗2+2𝜕2𝐹𝜕𝜎𝜕𝜗·dσdθ+𝜕2𝐹𝜕𝜎2𝜕𝜎𝜕𝜗2𝜕𝐹𝜕𝜎−1 E4型
正在推出方程。(3)和(4)到式 (2)给:
ϑ ̇=dθdσσ ̇,ϑ¨=dθdσσ¨+d2ϑdσ2σ ̇2,σ ̇=dσdθϑ ̇,σ¨=dσdθϑ¨+d2σdθ2ϑ ̇2𝜗̇=dθdσ𝜎̇,𝜗¨=dθdσ𝜎¨+𝑑2𝜗dσ2𝜎̇2,𝜎̇=dσdθ𝜗̇,𝜎¨=dσdθ𝜗¨+𝑑2𝜎dθ2𝜗̇2 E5型
它表示用于计算输出构件的速度和加速度的关系。
当给定机制的输出也是下一个机制的输入时,单个链接可以放入所谓的链中。链接求解的算法用变换块标记 Tk𝑇𝑘 如图所示图3.
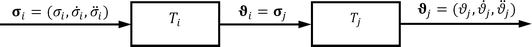
关于解决组合凸轮机构的问题,我们引入了以下主要构件的位置和运动学大小的命名法(名称)。变量 τ𝜏 分配给组合凸轮机构的驱动(输入)件。从动(输出)构件的位置用变量表示 w𝑤 .作为一个被驱动的成员,我们通常认为这样一个工作成员或一个机构,其价值观是解决方案的结果。凸轮相对于一般凸轮机构框架的凸轮位置由角度变量ψ确定,千斤顶的位置由广义变量 v 表示(参见图1).组合凸轮机构的计算过程通过框图显示,该框图由变换块组成 Tk𝑇𝑘 和转换块 C𝐶 (见图4).转换块 C𝐶 表示一般凸轮机构解的算法。从框图的结构来看,建议将变换块分为三组。它们由以下术语链标识:
- 输入链 我C集成电路 将机械系统的输入连接到模块的输入 C𝐶 .
- 输出链 OC超频 连接模块的输出 C𝐶 到机械系统的输出。
- 平行链 邮编个人电脑 由不属于先前链的块组成。
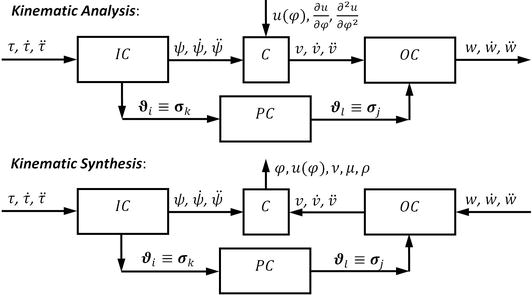
索引 i、j、k 和 l 表示 i第, J第、k第和 l第相关链条的联动。
组合凸轮机构任何构件的位置和运动量的计算被设计为运动学分析(参见框图图4).输入数据是关于机构、其链的计算过程、位移函数的典型数据(几何质量和尺寸) τ=τ(t)𝜏=𝜏𝑡 驱动部件的形状,以及凸轮的理论轮廓 u(φ)𝑢𝜑 .解的输出是机械系统所选构件的位移,由变量的三元组表示 w=(W,ẇ ,w¨)𝑤=𝑤𝑤̇𝑤¨ .组合凸轮机构的运动学合成用于计算径向凸轮的极坐标 φ、u 或轴向凸轮的圆柱坐标 φ、x、y。此外,通过合成,法向角度 ν𝜈 、压力角度 μ𝜇 和凸轮轮廓的曲率半径 ρ𝜌 已设置。任务的输入数据包括机械系统的数据、链条的计算程序、驱动构件的位移函数 τ=τ(t)𝜏=𝜏𝑡 ,并被驱动为系统的成员 W=W(t)𝑤=𝑤𝑡 .
2.3 位移定律
凸轮轮廓的形状是通过综合确定的,该综合基于给定组合凸轮机构的位移定律及其尺寸参数的知识。根据已发表的知识,提出了以下关于流离失所法的意见.
分配时间的函数 t𝑡 对机械系统给定成员的位置变量称为运动函数 w=f(t)𝑤=𝑓𝑡 该成员。因此,驱动部件的运动由独立运动函数描述 τ(t𝜏(𝑡 )和从动件的运动 W(t)𝑤𝑡 .位移定律表示从动件运动对组合凸轮机构的驱动件运动的功能依赖性 w=f(τ)𝑤=𝑓𝜏 .流离失所法 w(τ)𝑤𝜏 具有旋转输入构件的机械系统是周期为 2π2𝜋 .时期 2π2𝜋 可分为运动间隔和停留间隔。每个运动间隔的位移可能与最大总上升不同 W𝑊 和规范化形式的表达式 η=η(ξ)𝜂=𝜂𝜉 其中位移和范围是统一的(参见图5).变量 ξk𝜉𝑘 和 ηk𝜂𝑘 的 k第运动间隔与原始变量呈线性相关 τ𝜏 和 w𝑤 可以表示为
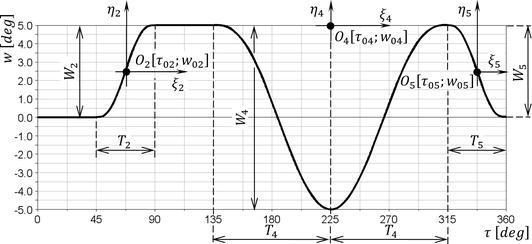
ξk=τ−τ0千米Tk,ηk=W(t)−w0千米Wk𝜉𝑘=𝜏−𝜏0𝑘𝑇𝑘,𝜂𝑘=𝑤𝑡−𝑤0𝑘𝑊𝑘 E6型
初始点 Ok𝑂𝑘 每个运动间隔上的位移由坐标定义 τ0千米𝜏0𝑘 , w0千米𝑤0𝑘 .自变量 τ 的区间长度由大小 Tk>0𝑇𝑘>0 ,最大升力由大小表示 Wk≷0𝑊𝑘≷0 .原始导数和归一化导数之间的关系是
DWdτ=WT⋅dηdξ=WT⋅η′(ξ),d2wdτ2=WT⋅η”(ξ)DW公司dτ=𝑊𝑇·dηdξ=𝑊𝑇·𝜂′𝜉,𝑑2𝑤dτ2=𝑊𝑇·𝜂′′𝜉 E7型
单位位移的导数 ξ𝜉 将由素数表示,索引 k𝑘 ,索引运动周期,被忽略。当变量 w𝑤 是一个函数 t𝑡 ,则导数将具有以下形式
DWDT=WT⋅η′(ξ)⋅dτDT=WT⋅η′(ξ)⋅τ ̇,DW公司DT型=𝑊𝑇·𝜂′𝜉·dτDT型=𝑊𝑇·𝜂′𝜉·𝜏̇,
d2wDT2=WT⋅[1T⋅η”(ξ)⋅(dτDT)2+η′(ξ)⋅d2τDT2]=WT⋅[1T⋅η”(ξ)⋅τ ̇2+η′(ξ)⋅τ¨]𝑑2𝑤DT型2=𝑊𝑇·1𝑇·𝜂′′𝜉·dτDT型2+𝜂′𝜉·𝑑2𝜏DT型2=𝑊𝑇·1𝑇·𝜂′′𝜉·𝜏̇2+𝜂′𝜉·𝜏¨ E8型
为了解决与凸轮系统的运动学分析和合成相关的问题,可以使用规范化形式的广泛位移定律。例如,这些位移包括多项式、三角形位移和指数位移以及摆线位移、抛物线位移和角位移.
位移定律的选择对高速机械系统的动力性能和行为有很大影响,在规定条件下应满足以下基本标准:
- 相对于机构所需的运动,凸轮机构的加速度惯性力、动量和性能应始终尽可能小。
- 机械系统运动所施加的振动应保持在最低限度。
由于动态效应,这两个标准都导致机械系统构件的动态应变较低。此外,第二个标准与遵守规定工作构件位置的准确性和消除任何噪声源有关。
3.凸轮和凸轮从动件的接触
在本文部分,我们将主要关注凸轮和滚柱从动件接触形成的一般运动学对。技术实践中提到的运动学约束类型通常通常由圆柱滚子和凸轮或冠形滚子和凸轮构成。在计算目的方面,我们可以用上述两种接触来代替圆柱体与平行轴的接触以及椭圆体与圆柱体的接触。
一般运动副的接触面积在工作循环内受到循环载荷,而接触面主要处于滚动接触状态,并结合少量的相互滑动。因此,实现了法向力和切向力的传递。这些现象导致两个物体在接触中变形,并在其中引起接触应力。工作表面及其下方的应力状态以主应力为特征,主应力是瞬态的,具有周期为 2π 的脉冲特征。凸轮和从动接触面的疲劳损伤可能在凸轮机构运行一定次数的循环后发生,只要在接触区域的任何点超过该应力的一定限值。这种损坏以空腔(点蚀)的形式出现,由工作表面的裂缝发展而来。对于具有硬化表面的凸轮,该层可能会断裂,然后剥落(剥落)(参见图6).这两种类型的损伤都是由于接触应力引起的,接触力学理论可以描述这种应力.因此,在估计一般运动对接触区域的寿命方面,减少的应力在表面积及其下一定深度的分布是一个重要标准。因此,在凸轮机构领域,主要是根据凸轮和从动件接触面的力载荷条件来确定其使用寿命。

两个弹性体在载荷作用下接触时存在的变形和应力状态既可以基于接触力学,也可以基于有限元法(FEM)的使用。接触力学涉及研究在一点或沿直线接触的固体在法向力和切向力作用下的应力和变形。物理和数学关系是在连续介质力学和材料力学知识的基础上制定的,重点是静态或动态接触中的弹性体、粘弹性体和塑体。接触力学原理用于解决滚动体(滚珠、滚子、桶、针、圆锥滚子)和滚子轴承套圈的接触、齿轮中齿的接触、铁路车轮和轨道的接触、机械约束,以及最后但并非最不重要的凸轮和凸轮从动件的接触问题。计算结果也是赫兹接触应力,其中接触区域存在局部应力,这是由两个弯曲区域的接触引起的,而这些应力由于作用载荷而略微变形。赫兹接触应力是制定方程的基本量,用于确定凸轮机构、轴承、齿轮和所有表面接触的物体的承载能力和疲劳寿命。
3.1 接触应力
当两个三维物体接触时,它们最初在单个点(凸冠滚子与凸轮接触)或沿直线(圆柱滚子与凸轮接触)接触。在最轻微的负载作用下 N𝑁 ,它们会变形,并且与两个物体的尺寸相比,在很小的有限区域内进行接触。在压缩过程中,两个物体的远距离点( T1和 T2)彼此相距一段距离 δ𝛿 .点 S1𝑆1 和 S2𝑆2 在接近的接触面上,弹性位移量 uz1𝑢𝑧1 和 uz2𝑢𝑧2 ,如图7.接触区域中每个表面的形状可以用两个变量中的齐次二次多项式来描述 [5]:
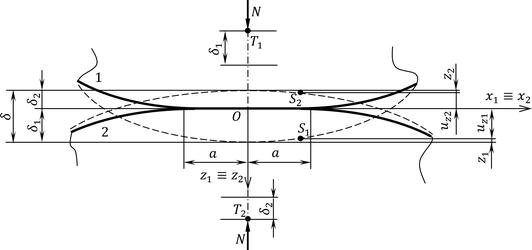
z我=∓12(1ρxix2+1ρyiy2),i=1,2𝑧我=∓121𝜌西𝑥2+1𝜌彝𝑦2,我=1,2 E9型
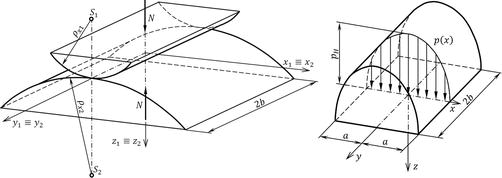
哪里 ρxi𝜌西 和 ρyi𝜌彝 是直角坐标系原点处曲面曲率的主要半径(请参阅图8).接触应力和变形满足平衡下均匀体、各向同性和弹性体的应力和应变的微分方程。接触面积上的压力分布由公式[5]给出:
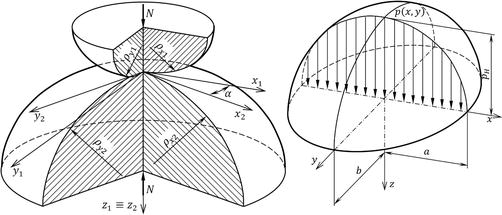
p(x,y)=pH1−(x一个)2−(yb)2−−−−−−−−−−−−−−√𝑝𝑥𝑦=𝑝𝐻1−𝑥一个2−𝑦𝑏2 E10型
哪里 一个一个 和 b𝑏 分别是椭圆接触面积的长半轴和短半轴,以及最大值 pH𝑝𝐻 称为赫兹压力。用有效弹性模量:
1E∗=∑我1−ν2我E我,i=1,21𝐸∗=∑我1−𝜈我2𝐸我,我=1,2 E11型
哪里 E我𝐸我 和 ν我𝜈我 是各自的杨氏弹性模量和单个固体的泊松比。
接触应力高度集中在接触区域附近,并随着距离的增加而迅速减小。因此,应力区域靠近身体接触。由于与主体的其余部分相比,接触面的尺寸较小,因此接触区域周围的应力既不太依赖于接触中主体的形状,也不太依赖于主体的安装方式。该假设简化了边界条件的定义,并允许应用大体弹性理论。
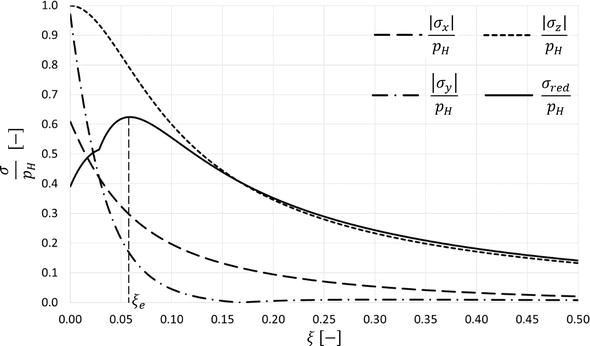
在凸冠滚子与凸轮接触以及圆柱滚子与凸轮接触的情况下,显然满足上述假设。因此,赫兹接触应力理论的结果可用于确定其接触区域和表面下一定深度的应力状态(参见 [5]) 或使用出版物中给出的与这些接触类型相关的结果 [3,6,7],或者我们可以使用网页上提供的计算算法直接计算点或线接触的接触应力 [8].在图8,有凸冠滚子和凸轮(左)的接触和接触应力在接触区域(右)的分布的示意图。类似的案例显示在图9唯一的区别是圆柱滚子和凸轮的接触。在这些情况下,应力状态由主应力表示 σx𝜎𝑥 , σy𝜎𝑦 , σz𝜎𝑧 并减轻压力 σRED𝜎红 .这些是普遍的压应力,它们的绝对值随着与表面的距离而降低。图10通常描述对称平面中各个应力的走向 ××××××××xz 依赖于深度 z𝑧 在表面之下。从减轻压力的过程中 σRED𝜎红 ,很明显,它的最大值在一定深度 ze𝑧𝑒 ,以单位形式表示 ξe𝜉𝑒 .校长强调 σx𝜎𝑥 , σz𝜎𝑧 在接触区域的物体表面达到它们的极值,并等于赫兹压力值。
确定物体接触区域应力的另一种可能方法是使用有限元方法。为了获得相关结果,需要在接触区域中建立密集的有限元网格。这一要求导致了大量求解的线性代数方程。计算体接触算法基于查找接触元素的数值迭代,因此赋值方程的数值解分几个步骤进行。
3.2 减轻压力
为了估计接触区域的寿命,首先需要确定减少应力的大小 σRED𝜎红 ,将其与应力极限值进行比较 σh𝜎ℎ .根据屈服抗拉强度确定的允许应力 R第0.2 页𝑅𝑝0.2 或极限抗拉强度 Rm𝑅𝑚 指单轴应力。因此,有必要有一个比较单轴应力和多轴应力的标准,以评估多轴应力下的强度。这些标准提供了强度假设。在延展性材料的情况下,破坏发生在拉应力处的最大剪切应力平面上。使用客人的假设(例如,参见 [9]).根据该假设,应力是从最高剪应力的角度判断的,该应力与主应力的最大差异成正比:
σRED=麦克斯{|σx−σy|,|σz−σx|,|σz−σy|}𝜎红=麦克斯𝜎𝑥−𝜎𝑦𝜎𝑧−𝜎𝑥𝜎𝑧−𝜎𝑦 E12型
主应力分量 σx𝜎𝑥 , σy𝜎𝑦 , σz𝜎𝑧 在条件中方程 (12)取决于一般运动学对的接触类型。这些组件必须在凸轮机构的整个操作周期内建立,以确定其最大值。图10表明降低应力的最高值在表面下一定距离处。为了计算主应力,可以对两个弹性体的相应接触使用接触力学的结论,但也可以使用有限元的方法.
在一般运动对的情况下,物体接触面及其下方的接触载荷具有周期性过程。在一般运动对的接触区域和这些点以下,接触应力成为与角凸轮位移相关的周期性大小 ψ𝜓 .这些瞬时应力的特征是具有周期性的脉冲 2π2𝜋 .在可变载荷作用下的强度条件如史密斯图所示(参见 [10]),其中平均应力由以下公式确定:
σm=12[麦克斯σ(ψ)+分钟σ(ψ)],ψ∈⟨0,2π)𝜎𝑚=12麦克斯𝜎𝜓+分钟𝜎𝜓,𝜓∈0,2𝜋 E13型
及其振幅由等式计算:
σ一个=12[麦克斯σ(ψ)−分钟σ(ψ)],ψ∈⟨0,2π)𝜎一个=12麦克斯𝜎𝜓−分钟𝜎𝜓,𝜓∈0,2𝜋 E14型
在方程。(13)和(14),变量 ψ𝜓 显示凸轮的旋转角度。可变载荷下的强度条件由应力极限给出σh这与暂时性应力引起的干扰一致。减轻应力 σRED𝜎红 (ψ,z)𝜓𝑧 受实际强度条件限制,写成[1]:
麦克斯σRED(ψ,z)<σh,ψ∈⟨0,2π),z≥0麦克斯𝜎红𝜓𝑧<𝜎ℎ,𝜓∈0,2𝜋,𝑧≥0 E15型
其中变量 z𝑧 是凸轮或滚子接触面下的深度。基于具有极限抗拉强度的钢的测试 Rm∈⟨500,1500⟩MPa𝑅𝑚∈5001500MPa的 ,受拉力加载的材料的疲劳极限假定为 σC≈0.35转米𝜎𝐶≈0.35马币 屈服强度为 R第0.2 页≈(0.55÷0.8)R米𝑅𝑝0.2≈0.55÷0.8马币 (参见 [1]).由于极限,瞬态应力的值,可以根据近似确定 σh≈σC≈0.7Rm𝜎ℎ≈𝜎𝐶≈0.7𝑅𝑚 ,则可以替换条件方程 (15)通过不等式 [1]:
麦克斯σRED(ψ,z)<R第0.2 页,ψ∈⟨0,2π),z≥0麦克斯𝜎红𝜓𝑧<𝑅𝑝0.2,𝜓∈0,2𝜋,𝑧≥0 E16型
条件不平等方程 (16)描述了在凸轮机构运行期间,一般运动学对中不会发生弹性变形的破坏性作用这一事实。
3.3 接触区域的使用寿命
凸轮和凸轮机构中从动件的加载接触区域损坏的标准是裂纹和空腔的形成,即所谓的点蚀。接触体表面点蚀形成的问题在于,由于形成的裂纹核在材料中随机分布,因此加载材料中裂纹的萌生和扩展是完全不可预测的。这种裂纹核是由这种材料的生产和处理引起的材料或表面不规则的夹杂物。因此,很难准确预测因负载而发生损坏的接触区域点的应力状态。这个问题可以通过引入一个标准来解决,该标准在物体的接触面积中确定最高主压应力的值,并将其与相应材料的极限强度联系起来。在纯滚动接触的情况下,其大小等于接触压力的最大值——赫兹压力 pH𝑝𝐻 .
在本文的前一部分,我们简要讨论了确定物体接触区域的表面和地下部分应力的方法。以下文本将提到两种理论方法,其中一种在 [1],另一个在[2].这两种过程都源于接触力学的知识,并在此基础上得出赫兹压力值pH在身体接触区域已经确定。这两种方法都需要进一步了解一些或几个参数,这些参数表征了制造凸轮的材料。这些特性参数并非适用于所有材料;因此,有必要使用实验程序。并非所有材料都可用于这些材料,因此需要进一步的实验程序。
在凸轮机构的运行循环过程中,在负载下接触面上不会因形成凹坑而造成的损坏。参考 [1],如果赫兹压力由尼曼经验关系给出,则不会发生这种疲劳损伤,其形式为:
pH≤KN1/6f(H),K=4777米𝑝𝐻≤𝐾𝑁1/6𝑓𝐻,𝐾=4777MPa的 E17型
其中变量 N𝑁 是数百万次循环的寿命, H𝐻 是接触中的表面硬度,以及其功能 f(H)𝑓𝐻 表示表面硬度对允许赫兹压力的影响 pH(MPa的)𝑝𝐻MPa的 .因素 K𝐾 是一个由经验确定的常数。表面硬度 H𝐻 与最大赫兹压力极限相关 pH麦克斯𝑝𝐻麦克斯 在操作周期中表示为 乙型乙乙型肝病 对于布氏和 HRC人权理事会 对于洛氏刻度。然后,对于函数 f(H)𝑓𝐻 ,则表述了以下经验关系:
f(H)=乙型乙1000,f(H)=0.251+HRC100[HRC100(2.74−1.22HRC100)−0.6]𝑓𝐻=乙型肝病1000,𝑓𝐻=0.251+人权理事会100人权理事会1002.74−1.22人权理事会100−0.6 E18型
这个标准方程 (18)非常简单,因为它依赖于唯一的材料参数 H𝐻 .
根据 [2],可以推导出应力水平的条件,其中身体的接触面不会损坏:
pH≤E∗145.03789⋅π(10ζN)1λ−−−−−−−−−−−−−√𝑝𝐻≤𝐸∗145.03789·𝜋10𝜁𝑁1𝜆 E19型
其中常数 E∗𝐸∗ 表征接触体的材料弹性,其定义如下方程 (11).在方程 (19)强度因素 ζ𝜁 和 λ𝜆 用对数坐标表示斜率和截距,即所谓的 S-N 图的应力轴,以表示相应材料的表面疲劳极限。S-N图是通过对大量测试数据进行回归分析来确定的。
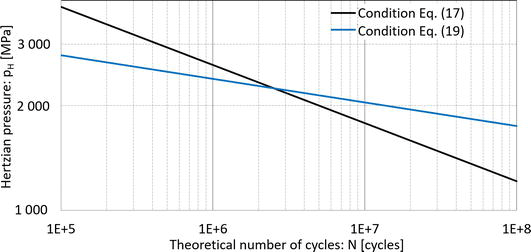
根据关系,两个条件方程。(17)和(19)以图形方式说明所选钢材 C22𝐶22 ( 10201020 , 1.04021.0402 ) 在图11.图形表示显示了上述理论在确定接触物体寿命方面存在相当大的差异。在有限寿命的区域,这是由损坏的循环次数给出的 N=107cycles𝑁=107周期 ,寿命测定的条件视条件而定方程 (19)通常与安全相关的程度高于条件方程 (17).在无限寿命的区域,即 N>107cycles𝑁>107周期 ,情况正好相反。在确定接触体寿命的两种方法中,其他钢也得出了类似的结论。
4.滚子冠形状对凸轮应力的影响
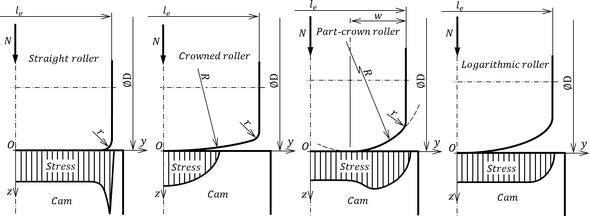
滚子冠本身的几何形状对应力分布有显着影响,这是由于一般运动副接触区域的载荷和惯性效应,通常在实践中由圆柱滚子和凸轮或冠形滚子和凸轮形成(见图12).
已经证明,形状附近的接触应力,接触物体接触区域的不连续性,远高于出版物中描述的在其直接影响区域之外达到的应力.因此,接触面受到更大的应力,并且其疲劳寿命缩短。
一般来说,通过使用滚子冠的圆柱形轮廓,我们可以期望实现任何凸轮机构的一般运动副的更长使用寿命。然而,在传统的直辊的情况下,滚子圆柱轮廓与凸轮轮廓的交汇处存在不连续性。这是由于一个接触区域轴向短于另一个接触区域以及滚子边缘倒角引起的。在这些轮廓不连续点附近,滚子和凸轮之间的接触不能简单地视为直线接触,而是一种更复杂的三维接触类型。因此,在这种情况下,不可能将赫兹接触理论的结论应用于接触应力分布的计算。这些不连续性导致接触区域中适当点的接触压力高度集中。事实上,接触压力分布的这些局部增加会超过给定材料的强度极限,从而导致接触区域的塑性变形、材料中残余应力的形成或钢的硬化。相关区域将更容易对接触表面造成疲劳损坏,例如点蚀或剥落。
为了保证滚子和凸轮接触区域的接触应力分布更均匀,需要修改滚子冠轴向截面的形状。这是冠状滚子实际应用的原因之一,当冠型材的曲率半径远远大于滚子的径向半径时(见图12).此外,我们可以很容易地补偿滚子和凸轮之间的使用错位,而不会导致接触应力分布发生根本性变化。然而,接触应力分布的最大集中是在接触区域的中间实现的,其后果与直辊的情况一样。
通过牙冠轴向横截面的这种形状,可以减少直轧辊边缘附近的过度接触应力,该形状包括每侧连接到它的直线和切线圆弧(参见图12).然而,滚子冠的这种形状导致从滚子的圆柱形段过渡到冠状段时产生一定浓度的接触应力。一般运动对接触区域不同载荷水平的应力均匀分布是通过滚子冠的对数轮廓实现的(参见 [11,12]).这种类型的滚子冠的特征在于根据对数函数,从其中心到边缘的轮廓单调地递减(参见图12).
这些事实将在带有圆柱形、冠状和部分冠状滚子的凸轮接触示例中得到证明,这些凸轮接触是使用有限元方法定义的.使用有限元方法形成一般运动对模型是基于一些假设,在此基础上推导出两个弹性体的赫兹接触理论(参见 [5]).主要假设是接触面积是连续的,并且比接触体的特征尺寸小得多。因此,接触区域附近的应力并不依赖于接触体的形状,也不取决于这些体的固定方式。此外,假设接触应力非常集中在接触区域附近,并且随着与接触区域距离的增加而迅速减小。因此,应力作用区域位于物体接触附近。通过这些基本假设,简化了边界条件的定义,并允许应用具有足够小变形的大物体的弹性理论。
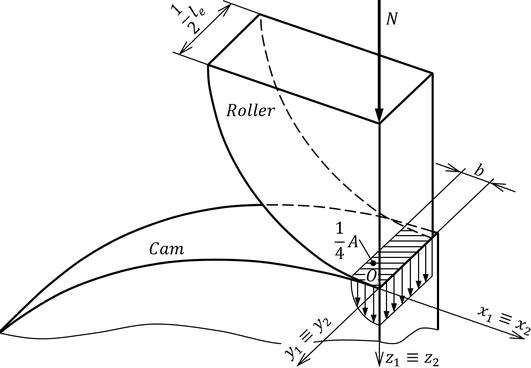
在创建凸轮机构的一般运动学对的有限元模型时,滚子与凸轮的接触将被两段旋转固体的接触所取代。旋转的固体之一代表具有所需成型轮廓的滚子,另一个具有圆柱形轮廓的滚子取代了凸轮。圆柱体的半径与凸轮与滚子接触点处的曲率半径相同。出于计算分析的目的,我们将使用它们中的每一个的八分之一,假设两个替换实体的轴平行度(参见图13).在 O××××××××𝑂xz 和 Oyz𝑂YZ的飞机符合图13,然后相应地定义了求解任务对称性的边界条件。具有凸轮含义的主体下表面是固定的,即该区域中主体有限元网格的所有节点都阻止了所有平移和旋转。通过边界条件的定义,允许滚子部分的上表面沿施加力的方向位移 N𝑁 ,即在 z𝑧 -轴 Oxyz氧氧 坐标系。还有武力的作用 N𝑁 均匀分布在该区域。
为了获得相关结果,重要的是使用均匀且密集的有限元网格来离散接触区域及其两个物体附近。元件的尺寸可以随着与接触区域距离的增加而逐渐增加。例如,根据赫兹的接触理论,可以预测接触面积的大小和形状,该理论应用于圆柱体与平行轴的接触或具有一般轮廓的物体与圆柱体的接触。利用这一理论,我们计算了接触区域及其接触体附近的变形和应力的分量。此外,接触区域的形状和尺寸取决于负载大小。这个问题已在文章中讨论过 [3,6,7]或详细发表在[5].然后,根据这样确定的数据,我们定义空间,以创建与真实状态相比的相应结果的分析体的可接受有限元网格密度。
上述程序的应用将在凸轮接触区域的接触应力分布分析中演示,其中标称尺寸是宽度 lCam=20毫米𝑙凸轮=20毫米 和曲率半径 RCam=50毫米𝑅凸轮=50毫米 在与相应滚轮的接触点附近。我们将考虑三种类型的滚子,其中标称尺寸根据图 12和13和表1.凸轮接触应力分析的目的是确定降低应力的最大可能值 σRED𝜎红 在凸轮的考虑部分取决于滚子的最大可能负载 N𝑁 .了解该应力值对于凸轮和从动件工作表面的疲劳损伤至关重要。凸轮和滚子的特征材料参数如下所述表2.
| 直辊 | 冠辊 | 部分冠辊 | ||
|---|---|---|---|---|
| 公称通径 | 直径[mm]𝐷毫米 | 35.0 | 35.0 | 35.0 |
| 有效宽度 | le[毫米]𝑙𝑒毫米 | 18.0 | 18.0 | 18.0 |
| 圆角半径 | r[毫米]𝑟毫米 | 0.6 | 0.6 | 0.6 |
| 冠半径 | R[毫米]𝑅毫米 | — | 500 | 200 |
| 冠宽 | 宽[mm]𝑤毫米 | — | — | 6.0 |
表 1.
滚子的标称尺寸。
| 滚筒:100Cr6 | 凸轮:16MnCr2 | ||
|---|---|---|---|
| 杨氏弹性模量 | E[GPa(英语:GPa)]𝐸GPa(英语:GPa) | 210 | 206 |
| 剪切模量 | G[GPa]𝐺GPa(英语:GPa) | 81 | 79 |
| 泊松比 | ν[−]𝜈− | 0.3 | 0.3038 |
表 2.
钢的材料特性。
重要结果总结如下:表3.根据接触区域的大小和最大降低应力的深度,定义该区域以在三种滚子和凸轮类型的接触附近创建高质量的单元网络,以使用 FEM 创建适当的模型。在凸轮和滚子与凸段的表冠接触的情况下,表中仅显示有限元分析的结果。图14显示了由所述凸轮滚子类型与凸轮接触引起的减少应力的分布。图15显示最大降低应力的过程,深度为 ze𝑧𝑒 根据与凸轮接触的所有滚子类型的凸轮宽度。深度 ze𝑧𝑒 表示刚好获得减小应力最大值的凸轮表面接触面积的距离。
| 直 | 加冕 | 部分表冠 | |||
|---|---|---|---|---|---|
| 负荷 | N[N]𝑁𝑁 | 40,000 | 15,000 | 35,000 | |
| 赫兹压力 | pH[MPa的]𝑝𝐻MPa的 | 2500 | 2400 | 2400 | |
| 最大程度地降低应力 | 赫兹理论 | 麦克斯(σRED)麦克斯𝜎红 [MPa的]MPa的 | 1440 | 1370 | 1480 |
| MKP系列 | 1970 | 1360 | |||
| 主要接触半径 | a[毫米]一个毫米 | — | 5.555 | — | |
| 接触半宽/小接触半径 | b[毫米]𝑏毫米 | 0.586 | 0.538 | — | |
| 最大减应力深度 | ze[毫米]𝑧𝑒毫米 | 0.42 | 0.38 | 0.38 | |
表 3.
结果摘要。
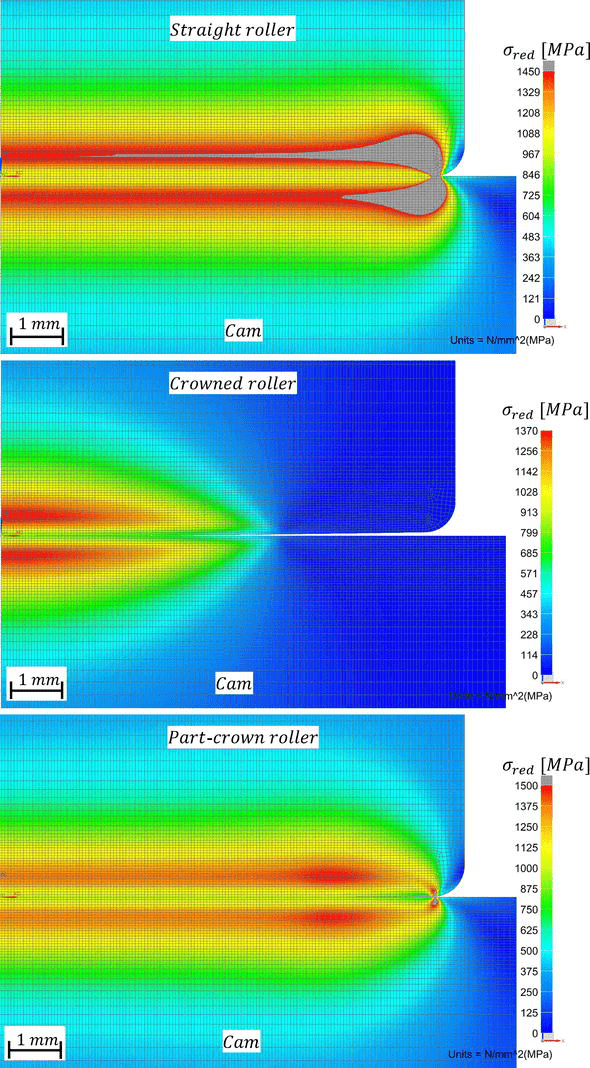
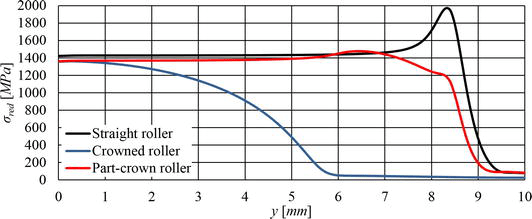
从表3和图 14和15,很明显,在剖面不连续点附近,减少的应力的大小有所增加。这一特点在圆柱滚子的情况下尤为明显,其中滚子和凸轮之间的接触不能仅仅被视为直线接触,而是一种更复杂的三维接触类型。因此,赫兹的接触理论不能应用于这种形状不连续性的接触。基于这一理论,与一般体与圆柱体接触以及两个圆柱体与平行轴接触区域内的有限元相比,效果非常好。此外,很明显,根据示意图,滚子冠的这种形状可以实现应力的均匀分布,其轮廓包括直线部分和两个圆形部分图12.这种滚子冠型材在负载传递能力和制造工艺方面具有优势。
5. 结论
本章提供了与一般运动学凸轮机构对相关的应力问题的基本信息。这种类型的运动学对由至少一个凸轮和一个从动件形成。一般的凸轮机构是一个非常简单的三件机械系统,可以非常精确地实现所需的工作运动。因此,它们被广泛用于制造业各种机器和设备的设计中。随着制造业对机械生产规模和质量的压力越来越大,对其性能、可靠性和使用寿命的要求也在不断增长。这一事实与机器在运行过程中的动态特性和行为的详细知识密切相关。因此,在一般运动学对中感应的动态响应既取决于所有机械系统的动力学特性,也取决于规定的位移定律。位移定律的选择应符合主要要求,例如减少自然振动、低动载荷、高定位精度和无噪音动作。
由于惯性和工作力的影响,一般运动学对中的感应力比是接触应变的原因。如果超过该应变的一定限值,凸轮和从动件接触面的疲劳损坏可能会在凸轮机构的运行中发生。因此,在设计凸轮机构时,了解接触应力的分布及其尺寸是必要的。以赫兹压力或主应力表示的接触应力成为确定上述运动学对工作区域寿命的标准。使用寿命本身取决于制造各个零件的材料的选择及其物理和机械性能,以及材料加工方式和单个零件的生产技术或负载的方式和强度。目前,凸轮和凸轮机构的凸轮从动件有多种材料可供选择。然而,在技术实践中,最常用的凸轮是由钢制成的。凸轮或凸轮从动件的表面可以进行热处理或化学热处理。处理的目的是实现凸轮机构接触区域所需的机械或物理化学性能。该程序的目的是提高接触面的硬度和抗磨损性,并保持相应部件的弹性芯。上述结果表明,有必要了解描述材料性能、热处理或其他工艺加工的各种特性参数,以便使用理论方法进行寿命估计。因此,实验方法是确定凸轮和从动件工作表面寿命的一个组成部分。
凸轮机构的一般运动副的工作表面经常在极端条件下工作,即高负载、高滑动速度和润滑条件差。因此,这一事实可能导致磨损或过度摩擦,从而降低使用寿命和效率。通过在凸轮和从动件的工作表面上涂覆涂层,可以减少这些影响。涂层是一种技术过程,包括将非常薄的层(数千毫米)施加到物体表面,与底层材料相比,该层具有相对较高的硬度和强度。涂层的薄层在相应部件的表层上形成所谓的屏障,防止其化学和物理机械磨损。涂层通常用于提高部件暴露表面层的硬度和摩擦性能、耐磨性和氧化性。这些涂层延长了滑动和滚动表面的使用寿命,有助于降低所需的功耗,同时提高性能。这减少了润滑剂的使用,并允许在相关机械的实施中使用新的材料组合。在某些情况下,涂层甚至是更高机械和热载荷的必要结构元件。
本文进一步提出了一种有效的凸轮机构一般运动学副动态接触应变分析方法,该方法包括两个物体之间赫兹接触理论的知识和结论的相互作用以及使用有限元方法的优点。使用赫兹的接触理论,我们预测了接触物体接触区域的形状和大小。通过这种方式,我们定义了该区域,以在接触附近创建适当大小的元素的均匀而精细的网格。考虑到赫兹理论的假设,一般运动对的有限元模型的定义大大简化,这减少了求解此问题所需的代数方程的数量;从而减少了计算时间。与真实状态相比,这种方法可以实现相关结果。该方法在确定滚子冠形状对凸轮应力的影响的任务中提出。
