探索有限元法 (FEM)、有限差分法 (FDM) 和有限体积法 (FVM) 的方法,以掌握它们在增材制造中的计算复杂性和特定应用优势。
有限元、有限差分和有限体积方法(分别为 FEM、FDM 和 FVM)是工程和机械设计中使用的数值技术,用于求解控制物理系统行为的偏微分方程 (PDE)。它们用于分析结构完整性、传热、流体动力学和其他物理现象,其具体用途基于几何形状的复杂性、所需的分析类型和所研究系统的性质。
本文将回答以下常见问题:
- 什么是有限元法?
- 什么是有限差分法?
- 什么是有限体积法?
- 每种方法的优缺点是什么?
什么是 FEM、FDM 和 FVM?
FEM、FDM 和 FVM 在重要方面彼此不同。了解这些区别是选择最适合您目的的方法的关键。
有限元法 (FEM) 解释
有限元法是一种计算方法,它将 CAD 模型细分为几何形状非常小但尺寸有限的元素。所有这些简单形状的集合构成了所谓的有限元网格。
下一步是采用一个场方程组,在数学上由描述您感兴趣的物理的偏微分方程表示,并为每个元素制定这些方程。这是通过将每个元素内的场近似为具有有限自由度 (DOF) 的简单函数(例如线性或二次多项式)来处理的。这通过一组简单的线性(但有时是非线性)方程给出了物理场的近似局部描述。当所有元素的贡献被组合在一起时,你最终会得到一个大的稀疏矩阵方程组,这个方程组可以由许多著名的稀疏矩阵求解器中的任何一个求解。
使用的求解器类型取决于原始物理场,因为每种类型的物理场都会在矩阵结构上留下其独特的印记。为了加快速度,通过使用定制的数值方法来利用这种结构。一种方法可能适用于结构力学,但不适用于电磁学,反之亦然。从历史上看,该方法首先应用于结构分析。自 2006 年以来,人们已经意识到有限元方法也适用于一大类多物理场问题。
了解有限差分法 (FDM)
有限差分法是离散化偏微分方程的最直接方法。您考虑空间中的一个点,在该点上获取方程的连续表示,并将其替换为一组离散方程,称为有限差分方程。有限差分法通常在规则网格上定义,这一事实可用于非常有效的求解方法。因此,该方法通常不用于不规则的 CAD 几何形状,而更常用于矩形或块状模型。
与有限元方法有联系:在正网格上定义的有限元方法的某些公式与同一网格上的有限差分方法相同。例如,规则网格通常可用于气象、地震和天体物理模拟。
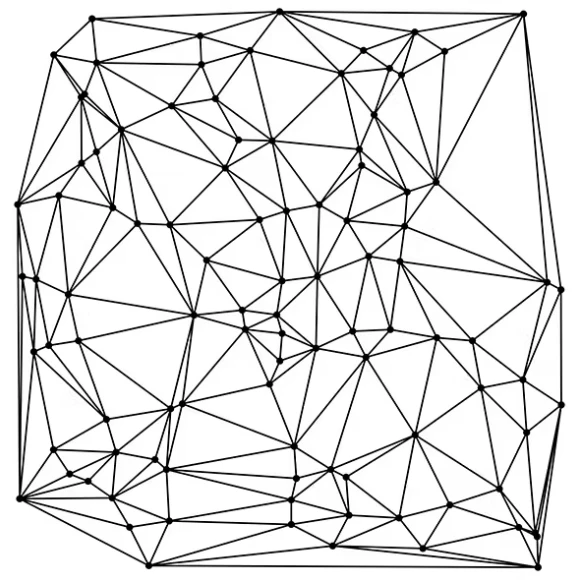
Delaunay 三角剖分用于为有限元和有限体积方法的空间离散化求解器构建网格。
有限体积法 (FVM) 概述
有限体积法与有限元法类似,因为 CAD 模型首先被划分为几何形状简单的非常小但尺寸有限的元素。除此之外,有限体积法与有限元法有很大不同,从元素的概念开始,元素被称为单元。
有限体积法基于这样一个事实,即许多物理定律都是守恒定律——进入一侧一个细胞的东西需要离开另一侧的同一细胞。按照这个想法,你最终会得到一个公式,该公式由通量守恒方程组成,该方程在单元上以平均值定义。从历史上看,这种方法在解决流体流动问题方面非常成功。
FEM、FDM 和 FVM 之间的主要区别
每种方法都非常相似,因为它们代表了求解偏微分方程的系统数值方法。一个重要的区别是易于实施。一个普遍的观点是,有限差分方法最容易实现,而有限元方法最难实现。其中一个原因可能是有限元方法需要相当复杂的数学公式。
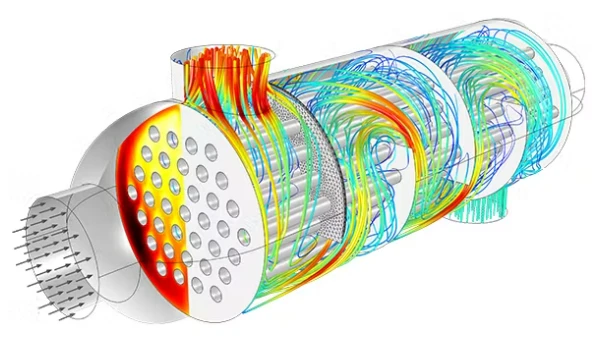
FEM:优点和缺点
有限元方法在多物理场分析中取得成功的一个原因是它是一种非常通用的方法。求解得到的方程组与用于结构和电磁学分析的众所周知的有效方法相同或非常相似。该方法成功的另一个原因是,它使“增加元素的顺序”变得容易,因此可以非常准确地近似物理场。这通常对应于使用“高阶”多项式(例如二阶和三阶多项式)或更高阶多项式局部逼近物理场。例如,在进行准确的应力分析时,这种技术通常至关重要。
如果我们考虑应力分析的例子,在机械零件的某些角落附近存在重要的应力集中是很常见的。在这种情况下,有限元方法允许使用两种不同的方法来提高该拐角处解的精度。一种方法是增加元素的顺序,如前所述。另一种方法是局部细化靠近该角的网格;元素密度局部增加。网格越细(即元素越多),对感兴趣角落周围的应力场的近似就越准确。这两种技术都用于有限元软件,并且从用户的角度来看通常是自动的。这称为“自适应网格细化”。
有限元方法的另一个优点是,可以组合不同种类的函数,这些函数近似于每个单元内的解。这称为混合配方。例如,在电磁加热的情况下,这一点很重要。物理和数学需要一种类型的电磁场函数和另一种类型的传热函数;它们都需要紧密耦合才能获得准确的解决方案并使解决方案收敛。混合公式很容易处理有限元方法,但使用其他方法则困难或不可能。
有限元方法和有限体积方法的优点是可以自然地处理弯曲和不规则的 CAD 几何体。
然而,有限元方法背后的数学非常先进,因此该方法需要数学专业知识才能实现。有限差分和有限体积方法的实现相对简单。
对于某些瞬态模拟,出于效率原因,需要使用所谓的显式求解器。对于有限元方法,实现这种求解器技术比对于有限差分和有限体积方法更困难。然而,在某些情况下,这已经成功地商业化,例如在碰撞模拟中。
FDM:优点和缺点
有限差分法是定义每个维度的维度;这使得增加“元素顺序”以获得更高阶精度变得容易。如果可以使用规则网格将仿真拟合到矩形或箱形几何体中,则与有限元和有限体积方法相比,高效实现要容易得多。如前所述,规则网格可用于超级计算机上的超大规模模拟,通常用于气象、地震和天体物理模拟。
使用有限差分方法时,在定义边界条件时,很容易遇到处理曲线边界的问题。需要边界条件来截断计算域。它们代表与周围世界的通信,这是您不希望包含在模拟中的部分。如果能够克服弯曲边界上的边界条件问题,则该方法可以得到非常有效和高质量的结果。
对于需要高精度的计算,在制作边界拟合网格方面付出的额外努力以及此类网格的实现的相关复杂性可能是值得的。示例包括一级方程式赛车计算流体动力学 (CFD) 仿真和航天飞机 CFD 仿真。有限差分法更难用于处理材料不连续性。此外,它不适合局部网格细化或类似于“自适应网格细化”的任何操作。如前所述,可能需要这样做来解决解决方案中的局部快速变化,例如在复杂形状的拐角处。
FVM:优势和劣势
有限体积方法是 CFD 问题的自然选择,因为您必须为 CFD 求解的偏微分方程是守恒定律。但是,有限差分和有限元也可用于 CFD。在过去的 10 到 15 年中,使用有限元方法的高效 CFD 技术变得越来越流行。使用有限差分和有限体积方法的 CFD 技术已经为人所知,并且使用时间要长得多。
有限体积法的优势在于它只需要对细胞边界进行通量评估。这也适用于非线性问题,这使得它对于稳健地处理传输问题中出现的(非线性)守恒定律格外强大。
有限体积方法(例如靠近感兴趣的角)的局部精度可以通过细化该角周围的网格来提高,类似于有限元方法。然而,当使用有限体积方法时,近似解的函数不能轻易地被高阶组成。与有限元法和有限差分法相比,这是有限体积法的缺点。
每种方法的应用
有限元的实际应用
各种结构分析、传热、化学工程、电磁学(包括静电学、静磁学、低频电磁学和频域高频电磁波)、多物理场和 CFD。
FDM 的用例
天气计算、天体物理学、地震学、计算机图形学中的物理现实主义和特效。
真实场景中的 FVM
CFD、传热和化学工程。
选择正确的方法
所有这些方法今天都经常用于商业软件以及学术环境中。有限元方法通常对计算机系统最费力,但这取决于分析的类型。
在凸轮分割器中的应用
对于凸轮分割器这类机械部件,它们通常涉及到结构强度、运动学和动力学分析。以下是这些数值方法可能的应用场景:
- 有限元法(FEM):可以用来分析凸轮分割器在工作过程中的应力分布、变形情况,以及评估其结构强度和耐久性。FEM特别适合处理凸轮分割器中的复杂几何形状和应力集中区域。
- 有限差分法(FDM):如果凸轮分割器的几何形状可以简化为规则网格,FDM可以用于求解控制凸轮运动的动力学方程,如速度和加速度分布。
- 有限体积法(FVM):在涉及流体动力或气动设计的凸轮分割器中,FVM可以用来模拟流体通过凸轮分割器时的流动情况,评估流体对凸轮的作用力。
在实际应用中,选择哪种方法取决于具体的分析需求、几何复杂性、计算资源和专业知识。对于凸轮分割器这类机械部件,FEM可能是最常用的方法,因为它能够提供详细的应力和变形分析,这对于设计和优化凸轮分割器的性能至关重要。
